Index
「未来の学びコンソーシアム」賛同企業
2020年度から、小学校でのプログラミング教育が必修化されます。
日本コンピューターサイエンス ( CSC ) は、「未来の学びコンソーシアム」 ( 文部科学省・総務省・経済産業省が連携して設立 ) の賛同企業です。
小学校の教職員を対象としたプログラミング教育のご提案
プログラミング的思考
プログラミング教育のねらいの一つに、「プログラミング的思考」の育成があります。「プログラミング的思考」とは、有識者会議「議論の取りまとめ」において説明されている、論理的思考力のことです。
- 文部科学省公表資料 「小学校プログラミング教育の手引(第三版)」
論理的思考力は、論理的思考のプロセスを繰り返すことによって、身についていくものです。
では、授業では何をどのように教えればよいのでしょうか。
当社が提案するプログラミング教育
日本コンピューターサイエンス ( CSC ) の社員研修では、論理的思考を以下のように教えています。
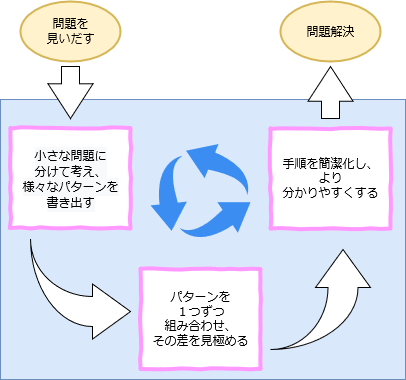
この研修を、小学校のプログラミング教育にかかわる教職員の皆様に受けていただき、児童に論理的思考のプロセスを教える際の一助としていただけましたら幸いです。
対象:小学校の教職員 ( プログラミング未経験者 )
プログラミング未経験でも心配ありません。当社では新人教育にも力を入れており、新人の中にはプログラミング未経験者もいます。このノウハウを活かし、未経験者にもわかりやすい研修をご提供します。
研修受講後、小学校で行っていただく想定の授業
対象学年
小学校4年生
学習内容
四則演算のフローチャートを作成する
学習活動の分類
C.教育課程内で各教科等とは別に実施するもの
※小学校段階のプログラミングに関する学習活動の分類
「小学校プログラミング教育必修化に向けて」パンフレット ( 未来の学びコンソーシアム作成 )
教材タイプ
アンプラグド
( パソコンなどは使用しません )
※ご希望に合わせて、ビジュアル型プログラミング言語 ( Scratch ) を利用した場合のプログラミングについてもご案内させていただきます。
使用教材
特別な教材は不要
研修例 ) 足し算のフローチャートを作成する
ここでは足し算の筆算を例に、どのように考えを進めていくか、ご紹介します。
以下のように段階的に考えながら、最終的に桁数の多い筆算にも対応できるフローチャートの作成を目指す、 という過程で論理的思考力を育みます。
フローチャートとは
処理の手順を図で表したものです。線をたどることで、処理の流れを追うことができます。
たとえば、クラスの児童を奇数月生まれ ( 赤組 ) ・偶数月生まれ ( 白組 ) の2組に分ける手順は、以下のようなフローチャートで表せます。

【分解】
| No | 条件 | 例 |
| ① | 繰り上げがない場合 | 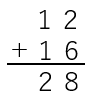 |
| ② | 繰り上げが1回の場合 ( 十の位への繰り上げがある場合 ) |
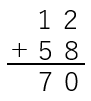 |
| ③ | 繰り上げが1回の場合 ( 百の位への繰り上げがある場合 ) |
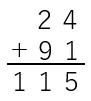 |
| ④ | 繰り上げが2回の場合 | 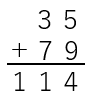 |
- 位をそろえて書く
- 一の位に答えを書く
- 十の位に答えを書く
- 百の位に答えを書く
- 一の位を計算する
- 十の位を計算する
- 十の位に1繰り上げる
- 百の位に1繰り上げる
【アルゴリズム的思考】
①繰り上げがない場合
②繰り上げが1回の場合
( 十の位への繰り上げがある場合 )
③繰り上げが1回の場合
( 百の位への繰り上げがある場合 )
④繰り上げが2回の場合
例_ア)
まず、①と②を組み合わせます。
次に、①と③を組み合わせます。
最後に、【5】【6】を組み合わせます。
例_イ)
まず、①と②を組み合わせます。
次に、【5】と③を組み合わせます。
